Was ist ein Korrelationsdiagramm? Kurz erklärt!
Das Korrelationsdiagramm, welches auch Streudiagramm genannt wird, stellt die Abhängigkeit von zwei Merkmalen zueinander grafisch dar. Die Merkmale werden hierbei als Wertepaar angegeben, welche im Diagramm als Punkte abgebildet werden. Aus dem entstandenen Punkte-Muster lassen sich anschließend logische Folgerungen zu einem möglichen statistischen Zusammenhang zwischen den beiden Merkmalen ableiten.
Das Streudiagramm stellt somit die Richtung und Intensität eines zu untersuchenden Zusammenhangs dar. Die Stärke des Zusammenhangs der Merkmale wird durch den Korrelationskoeffizienten angezeigt. Das Vorzeichen der Funktion zeigt die Richtung des Zusammenhangs an. So lässt sich beispielsweise anhand eines Korrelationsdiagramms auf einen Blick erkennen, ob ein Zusammenhang zwischen der Menge der in einem Betrieb produzierten Produkte und der festgestellten Fehlerquote existiert. Der Einsatz dieser Methode kann somit zur Steigerung von Prozess- und Produkteigenschaften im einsetzenden Unternehmen führen.
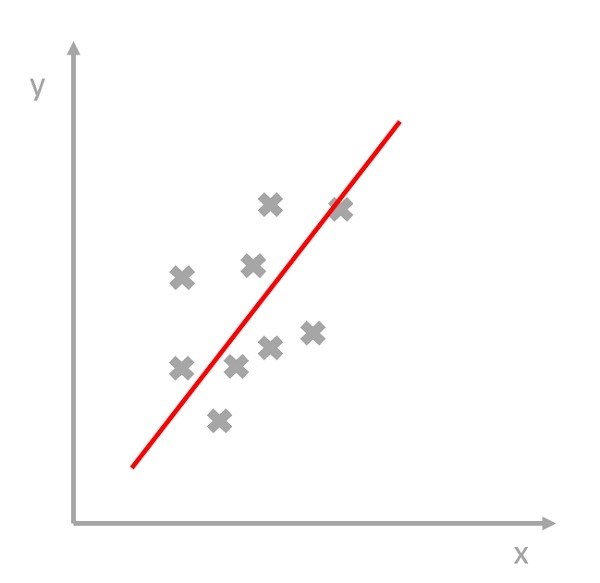
Um ein Korrelationsdiagramm zu erstellen, muss zuerst festgelegt werden, welche Merkmale auf einen vermutlichen Zusammenhang hin geprüft werden sollen. Damit das Diagramm ein aussagekräftiges Ergebnis liefert, sollten mindestens 30, besser jedoch 50 bis 100 Wertepaare erfasst werden. Wichtig hierbei ist es, dass alle Wertepaare immer unter der gleichen Bedingung ermittelt werden. Im nächsten Schritt werden die jeweils zum Wertepaar gehörenden Merkmale auf den zugehörigen Achsen eingetragen. Dadurch entsteht eine sogenannte Punktwolke. Lässt sich durch diese Punktwolke nun eine Gerade ziehen, so sind die Wertepaare korreliert. Falls sich durch die eingezeichneten Wertepaare keine Gerade ziehen lässt, so sind die Wertepaare unkorreliert. Anhand des Verlaufs der Geraden kann man erkennen, ob es sich eine positive oder negative Korrelation handelt. Steigt die Gerade nach rechts oben, handelt es sich um eine positive Korrelation. Fällt die Gerade nach rechts unten, handelt es sich um eine negative Korrelation. Je näher die einzelnen Punkte an der Geraden liegen, desto Stärker ist der Zusammenhang der untersuchten Merkmale.
Der Korrelationskoeffizient, also die Stärke des Zusammenhangs der untersuchten Merkmale kann durch die Eigenschaften und Größe der Stichprobe erheblich beeinflusst werden. Infolgedessen kann der Korrelationskoeffizient sowohl künstlich erhöht als auch gesenkt werden. Da Korrelationen für kleine Stichproben nur sehr wenig aussagekräftig sind, sollte unbedingt auf eine ausreichend große Menge der zu untersuchenden Wertepaare geachtet werden.
Hierbei ist jedoch zu beachten, dass die Korrelationsanalyse keine Aussagen zwischen den Wirkungszusammenhängen der Merkmale darstellen kann, sondern nur Aussagen über die Zusammenhänge der beiden verglichenen Merkmale treffen kann. Soll die Beziehung zwischen den beiden Merkmalen statistisch signifikant betrachtet werden, bietet sich hier eher die Durchführung einer Regressionsanalyse an.
Die Lösungsfabrik ist Professional Partner des TÜV Hessen Pareto-Diagramm
